Following are models
derived to, in theory, determine the important factors affecting
the coupling between an aerial telecommunication line and an
antenna. We will also try to find the main contributions to the
radiated electromagnetic field in different situations. Since
these models are going to be used in the study of xDSL signals we
will focus on frequencies up to 30MHz. The models are divided
into eight different coupling paths. They are initially divided
into four near-field models and four far-field models. The
near-field models, based on the mutual impedance, will have more
significant contributions to the coupling when the distance
between the emitting line and the receiving antenna r is much
less than 
and the
far-field models, based on the radiated field, will dominate when
the distance is much greater than 
(see Equation 43 to Equation 45). At
distances between the near-field and the far-field the
contribution will be a combination between the far-field models
and the near-field models.
Both the near-field models and the far-field models are divided into looking at the magnetic coupling or fields and the electric coupling or fields separately. This is because of the different characteristics of the two. All cases are finally divided into one model for the common-mode signals and one model for the differential-mode signals. For the common-mode signals, the signals on a two-wire line are approximated with one signal on a single conductor. In almost all cases the differential-mode models show much less tendency to radiate than the common-mode model, but since the differential-mode signals usually are of a much greater magnitude than the common-mode signals in a balanced transmission system, the contributions from the differential-mode signals can not always be neglected.
Notice that the far-field
is said to start at the distance 
if the size of the source, in this case
the length of the line D, is greater than a wavelength. This
has nothing to do with the different types of coupling, i.e. if
the induction terms or the radiation terms will dominate the
coupling (see Equation 43 to Equation 45). The distance is,
however, often used as the boundary between the near-field and
the far-field because at a shorter distance maxima and minima
would appear due to interference caused by different distances to
different parts of the source. That means that it is preferred to
do discrete measurements beyond this distance to get repeatable
results. The distance, r, is calculated for a couple of
line-lengths in Figure 16 below.
Figure 16 Distances to a far-field without fluctuations using a long line compared to the wavelength
The coupling between the telecommunication line radiating electromagnetic energy and a receiving antenna can be modeled with an equivalent two-port network as in the following figure:
Figure 17 Equivalent two-port network of the coupling between the telecommunication line and an antenna, with the antenna to the right and the coupling impedance Z12 (which is assumed to be equal to Z21)
The voltage on the line V1 principally represents the common-mode voltage of the line but could also be made up by differences in distance to the differential-mode voltages. I1 is the current in the telecommunication line and I2 is the current in the antenna. V2 is the voltage induced across the load impedance of the antenna. These voltages and currents are linearly related as:
 |
|
 |
Equation 116 |
where Z11, Z12, Z21 and Z22 are open circuit impedance coefficients. When the medium between the line and the antenna is bilateral, governing reciprocity relations, the coupling impedances Z12 and Z21 are equal. This equivalent network is used in the following theory only by the near-field models but it will hold for the far-field also since at large distances, r, between the line and the antenna, the coupling impedances will become very small:
 |
Equation 117 |
Then the impedances Z11 and Z22 will be nearly equal to the input impedances of the line and the antenna ZA and ZB. That means that with weak coupling Equation 115 could be written as:
 |
Equation 118 |
If we apply Thévenin’s theorem to the left of the load impedance of the antenna, ZL, we can determine the open-circuit voltage VOC and internal impedance Zg as:
 |
Equation 119 |
 |
Equation 120 |
Also here we can see that if we are in the far-field and have a weak coupling, the internal impedance, Zg, for the antenna will be approximately equal to its input impedance as:
 |
Equation 121 |
We can write the produced voltage and current in the antenna due to the current in the telecommunication line as:
 |
|
 |
Equation 123 |
These relations will be used in the following near-field models, where we look at the magnetic coupling considering the coupling impedance to be purely inductive and looking at the electric coupling considering the coupling to be purely capacitive. We will also look at common-mode signals and differential-mode signals separately.
The mutual impedance, Z12 or Z21, between two arbitrary positioned conductors above ground can be calculated according to the equations in Appendix C. These equations are however quite difficult to solve. There for we have decided to look at different situations to get simplified but restricted solutions.
In the near-field, the main coupling between a telecommunication line and an antenna is the mutual impedance, mainly consisting of mutual inductance from magnetic field coupling and mutual capacitance from the electric field coupling. The models for the near-field are divided in magnetic or electric coupling in which both common-mode coupling and differential-mode coupling are studied. The models are limited to looking at aerial telecommunication lines since they radiate more than buried cables, and represent a worst case situation. The results from each model could then be superimposed to determine the overall coupling. This can however produce errors when the length of the cable is much less than the wavelength. In our case this is almost always true. The purpose with the models will then be to find the main cause of radiation and the characteristic of the radiation in a particular case. This can be used to derive the important factors for this particular kind of radiation. Knowing these factors is very important when building realistic set-ups to measure the radiation and also when looking at different reduction techniques.
Notice that the results and reduction techniques can also be applied to cable-to-cable cross talk problems or antenna to cable disturbances.
5.1.1 Magnetic Coupling
5.1.1.1 Common-mode Coupling
In this chapter we will study the magnetic coupling of the common-mode current to an antenna due to mutual inductance, M, shown in the following figure:
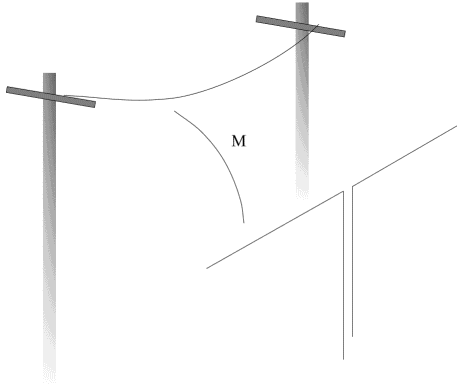
Figure 18 Common-mode magnetic (mutual inductance) coupling between a telecommunication line above and an antenna below. The common-mode current on the two wire line is approximated with one current on a single conductor.
The distance between the conductors is considered very small compared to the distance to the antenna. Therefore the two conductors carrying the common-mode current are considered as a single conductor.
The common-mode current in an aerial telecommunication line will follow a closed loop, denoted C1. The currents will follow the copper leads and then be coupled to ground via the common-mode impedance, which can be purely capacitive, and return in the ground-plane back to the source producing a closed loop bounding the surface S1. The common-mode current I1 flowing around the circumference C1 of S1, will produce a magnetic field B1. A part of the magnetic flux caused by B1 will link with the antenna, which bounds the surface S2. The mutual flux is then:
 |
If we take the surface integral of the fundamental postulate for electromagnetic induction (Equation 17) we get:
 |
Equation 125 |
where the left side is the induced electromotive force in the antenna, U2. Notice that C2 does not have to be a physical closed loop. The right side can be rewritten using Equation 124 and the result is the Faraday’s law of electromagnetic induction, which states that the electromotive force induced in a stationary closed loop circuit is equal to the negative rate of inverse of the magnetic flux linking the circuit [8]:
 |
Equation 126 |
Since the emf U2 is induced by a time-varying magnetic field it is called a transformer emf. The negative sign states that the induced emf will cause a current, which in turn will produce an opposite magnetic flux. This is known as Lenz’s law.
Then by using Biot-Savart’s law, which is obtained by taking the curl of the vector magnetic potential A (as in Equation 25 and Equation 26):
 |
where aR is the unit vector from the source point to the field point and R is the distance from the wire element dl to the field point. We can see that B1 is directly proportional to the common-mode current I1 and from Equation 124 we can see that the mutual flux F 12 is also proportional to I1. If we define that proportionality factor as the mutual inductance, M, between the telecommunication line and the antenna we have:
 |
which states that the mutual inductance is the magnetic flux linkage with one circuit per unit current in the other. In a similar way the self inductance is defined as the magnetic flux linkage per unit current in the loop itself as:
 |
For a linear medium, the self inductance does not depend on the current in the loop and exists regardless of whether the loop is open or closed. The inductances depend on the geometrical shape of the elements constituting the current and on the permeability of the medium.
If we consider the wire as one long conductor and a parallel dipole antenna as another long conductor where both conductors have the same radius, a, for simplicity reasons. These are separated by a distance d, which is much larger than a. Both conductors are in free space. To calculate the mutual inductance we first combine Equation 124 and Equation 128 into:
 |
Equation 130 |
where we use the subscript 1 to denote the telecommunication line and the subscript 2 for the antenna. Since B1 can be calculated from the curl of the vector magnetic potential A1 we can write (Equation 25):
 |
where the vector magnetic potential for a thin wire, using Equation 26, is:
 |
where R is the distance to the point of observation, in this case the distance between the telecommunication line and the antenna. Combining Equation 131 and Equation 132 we get the mutual inductance as:
 |
where we can see that in this situation the mutual inductance would vary inversely with the distance R between the antenna and the telecommunication line. We can also see that for a linear medium, it is proportional to the permeability and independent of the currents in the circuits. The contour integrals over C1 and C2 is however hard to calculate since the contour of a dipole antenna is non-obvious. Interchanging the subscripts would not change the value of the double integral which means that the reciprocity relations hold as discussed earlier, Z12 = Z21. Equation 133 is called the Neumann formula for mutual inductance.
The mutual inductance M as calculated in Equation 128 or Equation 133 would represent the value of a coupling inductor Z12 in Figure 17. The self-inductances, as calculated in Equation 129, would be part of the impedances Z11 and Z22 in the same figure. If Z12 is purely inductive then -Z12 in the upper impedances in Figure 17 would represent pure capacitances and the schematic in Figure 17 could be illustrated as in the following figure:
Figure 19 Magnetic coupling with the mutual inductance M
From Figure 19 we can clearly see the origin of the term mutual inductance, since both the current I1 and I2 are going through the same inductance M. From Equation 122 we get the induced current in the antenna as:
 |
The mutual inductance as illustrated in Figure 19 can also be illustrated as a transformer coupling using a lumped parameter circuit as in the following figure:
Figure 20 Equivalent circuit of the magnetic coupling between a telecommunication line above and an antenna below, showing the mutual inductance M and the self inductances L1 and L2.
U2 is induced emf in the antenna due to the common-mode current I1. The mutual inductance can be written as:
 |
Equation 135 |
where L1 is the self inductance of the telecommunication line, L2 is the self inductance of the antenna and the constant k is called the coefficient of coupling. This coefficient will depend on how much of the magnetic flux from the common-mode current that is coupled to the antenna. If there is no leakage flux this coefficient will be one, but in our case it will be much less than one. Using the circuit in Figure 20 the induced emf could be written as:
 |
which is directly proportional to the common-mode current. It also depends on the geometry by k and the self inductances of the telecommunication line and of the antenna.
We also know from Equation 133 that the mutual inductance vary inversely with the distance between the line and the antenna, R. We could extract the distance from the coupling coefficient, k, and define a new constant which will depend on the geometry of the loops only as K. Then we can rewrite Equation 136 as:
 |
5.1.1.2 Reduction of Common-mode Magnetic Coupling
The most obvious reduction techniques like reducing the loop area (i.e. reducing the height and the length of the telecommunication line) or increasing the distance, R, between the interfering and the interfered object is however hard to do in practice.
Reducing the common-mode current in the line will of cause have a direct effect on induced voltage in the antenna, as seen in Equation 137. Increasing the balance of the cable would reduce the common-mode current (see Equation 91). Increasing the common-mode impedance and the use of different common-mode rejection techniques could also be utilized to reduce the common-mode current.
The common-mode current is also reduced by reducing the differential-mode current since that is the source of the common-mode current. Operating at lower frequencies, if possible, would decrease the reactance of M.
5.1.1.3 Differential-mode Coupling
With differential-mode currents on the line, the two wires will cause almost equal and opposite magnetic fluxes that will tend to cancel each other. We denote the mutual inductance from one wire to the antenna M13 and the mutual inductance from the other wire to the antenna M23, as in the following figure:
The differential-mode currents are equal and have opposite direction. We can then write the induced current by using Equation 134 and the law of superposition:
 |
Equation 138 |
or with the emf-method as in Equation 136 (superposition):
 |
Equation 139 |
or with the distance extracted as in Equation 137:
 |
Equation 140 |
where we can see that if the mutual inductances are equal, there would not be an induced emf in the antenna. Due to slight differences in the distances between the antenna and the two lines and differences in the self inductances in the lines there will however be some coupling.
5.1.1.4 Reduction of Differential-mode Magnetic Coupling
The reduction techniques for reducing differential-mode magnetic coupling is based on getting the mutual inductance from the two wires to be as equal as possible. This is done by twisting the wire, which is equal to reducing the loop area between the wires. It is important to keep the wires as close as possible.
Also here we can see that the induced voltage in the antenna is directly proportional to the differential-mode current and varies inversely with the distance between the antenna and the line, R.
5.1.2 Electric Coupling
5.1.2.1 Common-mode Coupling
In this chapter we will study the electric coupling of the common-mode current to an antenna due to mutual capacitance, C, shown in the following figure:
As in the case of magnetic coupling, the distance between the conductors are considered very small compared to the distance to the antenna. Therefore the two conductors carrying the common-mode current are considered as a single conductor.
The capacitance between the telecommunication line and the antenna is a physical property. It depends on the geometry of the line and the antenna and of the permittivity of the medium between them. The capacitance of an isolated conducting body is the electric charge that must be added to the body per unit of increase in its electrical potential. The capacitance was defined from the observation that the ratio between the charge, Q, and the voltage, V, is a proportionality constant which remains constant.
 |
where the unit is coulomb per volt or farad, F. Recall that for a parallel plate capacitor of area S the capacitance C is expressed as:
 |
Equation 142 |
where d and 
are the distance
between the plates and the permittivity of the dielectric that
space.
Consider an infinitely
long line charge with a charge density 
[C/m]. It will cause a cylindrical
electric field with intensity E at the perpendicular distance r from
the line charge.
 |
Equation 143 |
This relationship can be used to approximate the electric field intensity of both the dipole antenna and the transmission line.
At a distance r from the line charge an electric potential can be calculated by integrating the electric field intensity E over the distance from the line charge to the point where the potential is to be calculated.
Figure 23 Cross section of a line charge, in P, and its image in a parallel conductor
If the equivalent diameter of the transmission line is approximately equal to the diameter of the dipole antenna wire, both diameters can be written as the same variable a.
The potential in the dipole antenna at a distance d from a line charge in the transmission line is:
 |
Equation 144 |
and the corresponding potential caused by a line charge in the dipole antenna is:
 |
Equation 145 |
If l is the length for which the transmission line and the dipole antenna are parallel, the mutual capacitance can simply be expressed as (using Equation 141):
 |
Equation 146 |
To use the mutual capacitance in the coupling impedance concept as in Figure 17, we have to rewrite the mutual capacitance coupling as a mutual inductance by assuming a very large resistance to ground as in the following figure:
Figure 25 Equivalent circuit of mutual capacitance, using mutual inductance instead
That the left side is the same as the right side in Figure 25 is realized when calculating the voltage out on the right, V2, from applying a voltage, V1, to the left (voltage dividing), first on the left circuit (in Figure 25):
 |
Equation 147 |
and then the same with the circuit to the right:
 |
Equation 148 |
The equivalent circuit will then be the same as in Figure 19 with the capacitance C as the value of M. The resistance 1/R will be neglectible compared to Z11 in Figure 19 since R is very large. Then we get the following relation of the current in the antenna due to the common-mode current in the telecommunication line (as in Equation 134):
 |
Equation 149 |
which is directly proportional to the common-mode voltage in the telecommunication line and to the capacitance between them. Notice that this current has the same sign as that from mutual inductance in Equation 134 and thus these two contributions will be additive and not cancel each other.
5.1.2.2 Reduction of Common-mode Electric Coupling
Since we can not control the antenna’s ground impedance, the only factors we can change are either the common-mode voltage or the capacitance between the line and the antenna. The capacitance is hard to reduce since we can not separate the line and the antenna or reduce the radius of the wires. A possibility is of course to operate at lower frequencies to increase the reactance caused by C. Reducing the common-mode voltage is done by increasing the balance of the cable (see Equation 91), increasing the common-mode impedance and the use of different common-mode rejection techniques (these methods also increases LCL as seen in Equation 101). The common-mode voltage is also reduced by reducing the differential-mode voltage since that is the source of the common-mode voltages.
5.1.2.3 Differential-mode Coupling
With differential-mode voltages on the line, the two wires will cause almost equal and opposite currents in the antenna which will tend to cancel each other. We denote the mutual capacitance from one wire to the antenna C13 and the mutual capacitance from the other wire to the antenna C23, as in the following figure
The current in the antenna due to the differential-mode voltages will then be:
 |
where I1 is the current in one conductor in the line and I2 is the current in the other conductor. But since these are differential currents only, I2 will have the same magnitude as I1 but opposite direction:
 |
Equation 151 |
Then we can write Equation 150 as:
 |
which is directly proportional to the differential-mode currents on the line and to the differences in mutual capacitance to the two conductors in the line. We can see that if the mutual capacitances are equal, the induced currents in the antenna will cancel each other. Due to slight differences in the distances between the antenna and the two wires and differences in the geometry between the two wires, there will however be some nonzero capacitive coupling even here.
5.1.2.4 Reduction of Differential-mode Magnetic Coupling
The most common reduction technique is to twist the wires to keep them as close as possible to each other. Reducing the differential-mode currents on the line will have a direct effect as seen in Equation 152. Equal diameters of the wires are important. The frequencies should be kept as low as possible. Separating the antenna and the line is very favorable, but hard to accomplish.
In the far-field the main cause of coupling between a telecommunication line and an antenna is the radiation term as derived in chapter 3. We chose here to look at the electromagnetic fields generated instead of the inductive and capacitive coupling as in the near-field models. The models are divided into magnetic fields from current loops and electric fields from time-varying voltages. These models are divided into common-mode radiation and differential-mode radiation. The results could, with care, be superimposed, but the purpose is to locate the main cause of radiation in a particular case as with the near-field models. Also here it is very important to know the main factors in each type of radiation to be able to build a realistic case for measuring, or to know which factor to focus on to reduce a specific kind of radiation.
In the models for both the magnetic and the electric radiation we will focus on a straight aerial telecommunication line as shown in the following figure:
Figure 27 The main radiation direction and polarizations for a rectangular loop
5.2.1 Magnetic Fields
5.2.1.1 Common-mode Radiation
In this chapter we will study the magnetic radiation due to common-mode current flowing as shown in the following figure:
Figure 28 The common-mode current loop causing magnetic fields, with aerial telecommunication lines. The common-mode signals on the two wire line are approximated with one signal on a single conductor.
As before the distance between the conductors are considered very small compared to the distance to the point of observation. Therefore the two conductors carrying the common-mode current are considered as a single conductor carrying a current.
Consider a small loop of radius b carrying a uniform time-harmonic current i(t)=Icosw t around its circumference as in the following figure:
This is called an elemental magnetic dipole, which has a vector magnetic moment, m, as:
 [Am2] |
Equation 153 |
To determine the electromagnetic field from this current loop, we need the vector magnetic potential, A, since the magnetic flux density, B, is the curl of the vector magnetic potential. Assuming that we have a thin wire and the current is flowing entirely along the wire we have:
 |
Equation 154 |
This integral is however hard to calculate exactly, because R1 will change with the location of dl’ on the loop. If we assume that we have a small loop we can solve the vector magnetic potential as:
 |
Equation 155 |
Then the electric and magnetic field intensities, E and H, can be solved by deriving the magnetic flux from the vector magnetic potential, A, for the magnetic field and then the electric field can be calculated from the curl of the magnetic field intensity as:
 |
Equation 156 |
 |
Equation 157 |
From this we get the electric and magnetic field intensities as:
 |
Equation 158 |
 |
Equation 159 |
 |
Equation 160 |
Notice the similarity with the equations for the electric dipole, derived in Equation 43, Equation 44 and Equation 45, and that the nature of the near and far-field discussed earlier also applies to these equations. For the far-field (R >> l /2p ) these equations will simplify to:
 [V/m] |
|
 [A/m] |
where w =2p c/l . We can see that the far-field intensities vary inversely as R and their ratio Ef /Hq equals the intrinsic impedance of free space, h 0. We can also see that the maximum fields are produced in the same plane as the current loop, where q is p /2.
The vector magnetic moment, m, is the current, I, times the area of the loop which we denote S. That means that the electric (and the magnetic) field intensity vary linearly with the current in the loop and the area of the loop. If we look at the electric field intensity in a point in the same plane as the loop, in the x-y plane, where we have the maximum field intensity, we could write the electric field intensity as a constant depending only on the frequency and the distance R times the current and the area of the loop (in free space):
 |
where the area, S, is in m2 and the current, I, is the peak amplitude current in amperes at appropriate frequency, then the constant K is derived as [5]:
 |
Equation 164 |
The current loop can be either a small loop or a large loop which will affect the input impedance of the loop and there for the current flowing in the loop. We have earlier derived the input impedance for a transmission line (Equation 82) repeated here:
 |
Equation 165 |
If we consider an ideal transmission line and assume negligible line losses it can be shown that the input impedance can be written as:
 |
where Z0 is the characteristic impedance of the line, ZL is the load impedance, l is the length of the line and l is the wavelength as in the following figure:
Figure 30 The input impedance for a line of length l
From Equation 166 we can see that for small loops with l << l (often written as l < l /10) we will have the input impedance, Zi, almost equal to the load impedance, ZL. If we have the line as illustrated in Figure 30 we will have a current in the circuit as:
 |
Equation 167 |
At low frequencies or short lines where we have a small loop, the current is essentially uniformly distributed around the loop. When the length become a significant fraction or multiple of the wavelength, the loop becomes a large loop. Since the input impedance vary with the frequency and the length of the line there will be a corresponding variation in the amplitude of the loop current. The input impedance will vary between maximum and minimum values depending on the relationship between the wavelength and the length of the cable or the circumference of the loop. The current distribution along the telecommunication line is generally in the form of standing waves with current maxima and minima along the line resulting in directional radiation field patterns. The amplitude of the standing waves is determined by the match between the characteristic impedance of the line and the load impedance.
Notice that in the common-mode situation, the load impedance is the common-mode impedance, which could be reactive (capacitive coupling to ground). If the load impedance is purely reactive, ZL=jXL, then the input impedance can be written as:
 |
and we will have a purely reactive input impedance with poles and zeros at different frequencies depending on the relation between the line length, load impedance and the characteristic impedance of the line.
If we look at the common-mode current loop as illustrated in Figure 28 we know that the electric and magnetic field intensity in the far-field is proportional to the loop area which is the medium height over ground times the length of the line and to the common-mode current flowing in the loop. Notice that in the aerial telecommunication line case, the loop will often become a large loop.
5.2.1.2 Reduction of Common-mode Magnetic Radiation
The most obvious way would be to reduce the loop area by reducing the height over ground or reducing the length of the cable, but since this would be to expensive, the reduction techniques are focusing on reducing the common-mode current amplitude. This is mainly done by reducing the ground loop coupling. The ground loop coupling can be reduced by on or more of the following techniques:
Shielding the loop area by grounding it is, at present, quite expensive. We can see that a buried cable would not have as large loop area as an aerial telecommunication cable. So if burying the cable is too expensive, the only way to reduce the radiation is to have as good balance as possible to reduce the amount of common-mode current and then to make it as hard as possible for the common-mode current to flow around the loop.
5.2.1.3 Differential-mode Radiation
The theory presented above for common-mode signals will hold in this case too except for the fact that the loop area will be much less than in the case of common-mode current in aerial cables. The loop area for the differential mode signal will be the area between the conductors of the cable, as illustrated in the following figure:
Figure 31 The differential-mode current loop causing magnetic fields.
Note that this area will be even less in a real cable since the cables are twisted, intentionally or unintentionally. The different parts of a twisted cable will not radiate in the same direction and will in some cases tend to cancel each other. Also what was said about the input impedance, see Figure 30, depending on the length of the cable can be applied to this situation, see Equation 166 and about the maxima and minima in Equation 168.
5.2.1.4 Reduction of Differential-mode Magnetic Coupling
Also here the radiation will be proportional to the current in the loop, see Equation 163, which means that a reduction of the differential-mode current would have a direct effect on the amount of radiated fields, by the same amount. It is also direct proportional to the loop area, Equation 163, and inversely proportional to the distance, R, to the point of observation (Equation 161 and Equation 162).
The most common reduction technique is the use of twisted pairs. The reduction of the differential mode coupling that is offered by twisted pair can be written as [8]:
 [dB] |
where n is the number of twists per meter, l is the length of the wire in meters and l is the wavelength in meters. The reduction of differential-mode coupling offered by twisted pair is plotted in the following figure:
Figure 32 Differential-mode coupling reduction offered by twisting wire pair
The x-axis is the total number of twists along the whole wire and each curve corresponds to the product of the number of twists per meter, n, and the wavelength, l .
5.2.2 Electric Fields
5.2.2.1 Common-mode Radiation
A two wire communication line carrying a common mode signal can be approximated as a single conductor carrying a signal. To be able to derive the far field radiation from such a line, it is modeled as a composition of many short conducting elements. The length of each element should be only a fraction of the wavelength of the signal in the conductor so that the current distribution within each element can be assumed to be uniform. We can now use Equation 43, Equation 44 and Equation 45 to calculate the radiation from each element. However since we in this part are only interested in the far field radiation (R>>l /2p ) the contribution to the far field radiation from each element can be calculated according to the following simplified equations:
 [A/m] |
Equation 170 |
 [V/m] |
By examining the relationships in these equations we see that the magnitude of the fields in the far field is proportional to the current through the element I, the length of the element dl and inversely dependent of the distance R and that the ratio between Eq and Hf equals the intrinsic impedance of free space, h 0. Another important observation is that the magnitude of the field is maximized perpendicular to the conducting element where q =p /2, and minimized along the axis of the conducting element where q =0, see Figure 3.
Consider a typical aerial telecommunication line with horizontally and vertically oriented segments according to Figure 33. According to the theory above, the common mode current will produce an electromagnetic field. The current distribution will also give rise to a charge distribution that also will produce an electromagnetic field. The value of the common-mode impedance will decide whether the common-mode current or the common-mode voltage will be the main cause of radiation.
Figure 33 The model for the electric fields generated by common-mode signals on the line. The common-mode signals on the two wire line are approximated with one signal on a single conductor.
The distribution of currents along a telecommunication line above a perfectly conducting ground has a corresponding image of an opposite current distribution equidistant to, but at the opposite side of the ground plane. This is called method of images. The vertical segments (down leads) in Figure 33 represent the common mode current path to ground. This path may consist of a capacitive coupling as well as a conductor and a common-mode impedance.
If the common-mode impedance is relatively small then the resulting radiation is mainly due to currents. Radiation caused by common-mode currents in the horizontal oriented segment of the line and its image will tend to cancel each other at some point in the far-field where the distance to the line and its image is equal or differs by a multiple of a wavelength. Since we are only interested in the fields at almost ground level the distance to the line and its image will be almost equal and the fields will cancel, see Figure 34 below.
Figure 34 Simulated electric fields from a telecommunication line above ground using the method of images
If the horizontal telecommunication line is several wavelength long and properly terminated it behaves as a traveling wave antenna with the current distribution:
 |
Equation 172 |
At points where the distance to the line and its image differs by an uneven fractions of a wavelength, radiation will occur.
Figure 35 Radiation pattern of a traveling wave antenna (q is the elevation angle above earth)
Again, this is not the case at ground level in the far field.
If the common-mode impedance instead is relatively large then the resulting radiation is mainly due to the charge distribution. In this case the radiation caused by the potential of the horizontal oriented segment of the line and its image will form a electrical dipole radiating a vertical polarized electric field.
Instead of expressing the electric field in terms of current distribution, as in Equation 171, a time varying field can be expressed in terms of charge distribution as:
 |
where
 |
Equation 174 |
 |
Equation 175 |
To be able to derive the electric field intensity in the far field we need to integrate Equation 173 to get:
 |
The capacitance per unit length between the telecommunication line and earth can be calculated as:
 |
Equation 177 |
where D is the average equivalent cable diameter of the telecommunication line and h is the height of the line above earth. This results in that an aerial telecommunication line of length L will have a total capacitance to earth of:
 |
The fundamental expression for a charge
 |
Equation 179 |
can by substitution, using Equation 178, be rewritten as:
 |
Equation 180 |
By examining Equation 176 we can identify a dependence of the derivative of the charge. The derivative of the charge can be written as:
 |
Equation 181 |
This is illustrated in the following figure:
Figure 37 A telecommunication line over ground acting as a vertical dipole
It can can also be expressed in terms of the potential V and the capacitance per unit length of the telecommunication line.
 |
Equation 182 |
This can be used to express the radiation as:
 |
A quick analyze of Equation 183 confirms that the electric field intensity in the far field will increase when:
The resulting magnitude of the radiation will at ground level also depend on the azimuth angle to the communication line. Perpendicular to the line the magnitude will be maximized and in parallel with the line the magnitude will depend on the distance between the down leads in relation to the wavelength as in the situation of a two element antenna array.
The dependence of the distance between the communication line and the observation point can also be calculated as the free space propagation loss. By assuming that far-field propagation and a spherical wave front applies and neglecting effects on the propagation of polarization, antenna heights, curvature of earth, atmospheric conditions, reflections and interfering objects along the path, the free space propagation loss can be approximated with the following formula, also shown in Figure 38.
 [dB] |
Equation 184 |
where FSPL is the Free Space Propagation Loss, R is the distance to the point of observation and f is the frequency in MHz.
Figure 38 The Free Space Propagation Loss
Notice that this is intended only to be used as a rule of thumb when evaluating the propagation loss at a distance from the source.
5.2.2.2 Reduction of Common-mode Electric Radiation
The signal source will ideally only produce differential-mode signals, common-mode signals will then arise from differential-mode signals due to longitudinal conversion loss (Equation 91). Hence, a way to reduce the common-mode electric radiation is to increase LCL (increase balance) to prevent conversion from differential-mode signals to common-mode signals. There will however always be some remaining common-mode signal that will cause radiation. To minimize the electric radiation we then have to reduce the common mode impedance, an undesired consequence of this is that the magnetic radiation will increase.
5.2.2.3 Differential-mode Radiation
The electric field radiation due to differential-mode signals is caused by opposite charges in the two wires of the telecommunication line.
Figure 39 The model for the electric fields generated by differential-mode signals on the line.
The theory for common-mode radiation above applies to this case too, if we consider having the opposite charges located in the two wires instead of in the line and its image. This will cause the distance between the opposite charges to be much smaller in this case for an aerial communication line. The capacitance between the two wires (Equation 65) is larger than the capacitance between the line and earth. As in the case of differential-mode magnetic radiation in the far field the magnitude of the radiation is also dependent on how the telecommunication line is twisted. As in illustrated in Figure 7 the electrical fields generated from the two conductors will tend to cancel each other.
5.2.2.4 Reduction of Differential-mode Electric Radiation
Because of the similarities with the case of differential-mode magnetic field radiation in the far field, the same reduction techniques are applicable. Twisting the cable is the best reduction technique (Equation 169).
Previous: Transmission Line | Next: Scale modelling
EMC of Telecommunication Lines
A Master Thesis from the Fieldbusters © 1997
Joachim Johansson and Urban Lundgren